Stress testing different find_paths() implementations on maximally connected graphs
Before trying the code in this section, make sure that you have created the "edges" table (see cr-edges.sql) and installed all the code shown in the section Common code for traversing all kinds of graph. Make sure that you start by choosing the option that adds a tracing column and a trigger to the "raw_paths" table. (You will later re-create the "raw_paths" table without the tracing code before you do some timing tests.)
Definition of "maximally connected graph"
Look at this undirected cyclic graph:
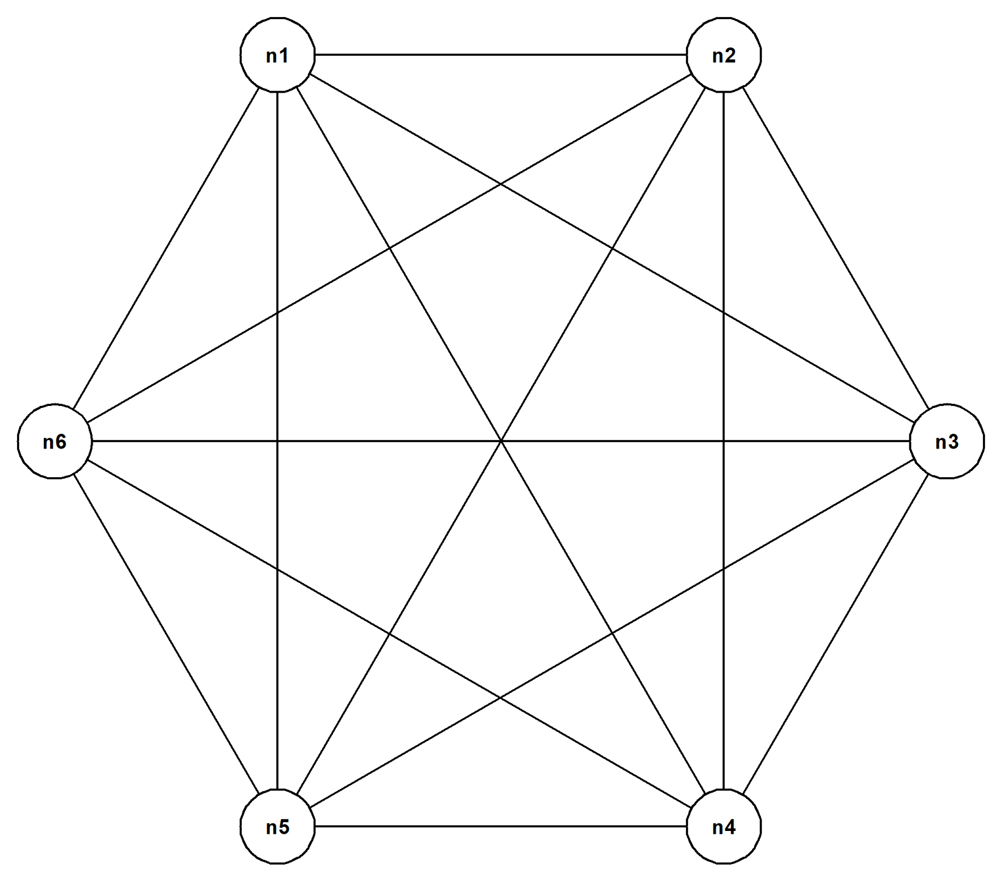
Each of its six nodes has an edge to each of the other five nodes—in other words, it's maximally connected.
A "maximally connected graph" is a connected undirected graph where every node has an edge to every other node. Such a graph is inevitably cyclic.
("Connected" means that there exists a path from every node to every other node in the graph.)
The following code automates the creation of such a maximally connected undirected cyclic graph for the specified number of nodes. First create a helper procedure:
cr-populate-maximum-connectvity-edges.sql
drop procedure if exists populate_maximum_connectvity_edges(int) cascade;
create procedure populate_maximum_connectvity_edges(nr_nodes in int)
language plpgsql
as $body$
declare
o constant text := '(''n';
p constant text := ''', ''n';
c constant text := '''),';
stmt text not null := 'insert into edges(node_1, node_2) values';
begin
for j in 1..nr_nodes loop
for k in j..(nr_nodes - 1) loop
stmt := stmt||
o||ltrim(to_char(j, '009'))||
p||ltrim(to_char(k + 1, '009'))||c;
end loop;
end loop;
stmt := rtrim(stmt, ',');
execute stmt;
end;
$body$;
Now invoke it to populate the "edges" table and inspect the outcome:
delete from edges;
alter table edges drop constraint if exists edges_chk cascade;
alter table edges add constraint edges_chk check(node_1 <> node_2);
call populate_maximum_connectvity_edges(nr_nodes=>6);
-- Implement the denormalization.
insert into edges(node_1, node_2)
select node_2 as node_1, node_1 as node_2
from edges;
select node_1, node_2 from edges order by node_1, node_2;
This is the result:
node_1 | node_2
--------+--------
n001 | n002
n001 | n003
n001 | n004
n001 | n005
n001 | n006
n002 | n001
n002 | n003
n002 | n004
n002 | n005
n002 | n006
n003 | n001
n003 | n002
n003 | n004
n003 | n005
n003 | n006
n004 | n001
n004 | n002
n004 | n003
n004 | n005
n004 | n006
n005 | n001
n005 | n002
n005 | n003
n005 | n004
n005 | n006
n006 | n001
n006 | n002
n006 | n003
n006 | n004
n006 | n005
The whitespace was added by hand to group the results into the sets of five edges that connect to each of the six nodes.
The number of paths in a maximally connected graph grows very much faster than linearly with the number of nodes
Recall how the logic of the recursive CTE from cr-find-paths-with-nocycle-check.sql is expressed:
with
recursive paths(path) as (
select array[start_node, node_2]
from edges
where
node_1 = start_node
union all
select p.path||e.node_2
from edges e, paths p
where
e.node_1 = terminal(p.path)
and not e.node_2 = any(p.path) -- <<<<< Prevent cycles.
)
Using node "n001" as the start node for the six-node example maximally connected graph, the result of the non-recursive term will be five paths. Then, the result of the first repeat of the recursive term will be four longer paths for each of the input five paths because the cycle prevention logic will exclude, for each input path in turn, the node that can be reached from its terminal that has already been found. And so it goes on: the result of the next repeat of the recursive term will be three longer paths for each input path; the next result will be two longer paths for each input path; the next result will be one longer path for each input path; and the next repeat will find no paths so that the repetition will end. The number of paths that each repetition finds will therefore grow like this:
Repeat number Number of paths Found
0 5 -- non-recursive term
1 5*4 = 20 -- 1st recursive term
2 5*4*3 = 60 -- 2nd recursive term
3 5*4*3*2 = 120 -- 3rd recursive term
4 5*4*3*2*1 = 120 -- 4th recursive term
---
Final total number of paths: 325
You can see this in action by re-creating the "find_paths()" implementation shown in cr-find-paths-with-pruning.sql and invoking it like this:
call find_paths(start_node => 'n001', prune => false);
Now inspect the repetition history:
select repeat_nr, count(*) as n
from raw_paths
group by repeat_nr
order by 1;
This is the result:
repeat_nr | n
-----------+-----
0 | 5
1 | 20
2 | 60
3 | 120
4 | 120
This agrees with what the analysis presented above predicts.
The following function implements the rule described above to compute, for a maximally connected graph, the total number of paths from an arbitrary start node versus the number of nodes in the graph. It follows from the definition that the number of paths for a particular graph is the same for every possible start node.
cr-total-paths-versus-number-of-nodes.sql
drop function if exists total_paths_versus_number_of_nodes(int) cascade;
create function total_paths_versus_number_of_nodes(nr_nodes in int)
returns table(t text)
language plpgsql
as $body$
begin
t := 'no. of nodes no. of paths'; return next;
t := '------------ ------------'; return next;
for j in 4..nr_nodes loop
declare
-- Non-recursive term result
new_paths numeric not null := j - 1;
total numeric not null := new_paths;
begin
-- recursive term repetitions.
for k in 1..(j - 2) loop
new_paths := new_paths * (j - k - 1)::bigint;
total := total + new_paths;
end loop;
t := case total < 10000000
when true then
lpad(to_char(j, '9999'), 12)||lpad(to_char(total, '9,999,999'), 15)
else
lpad(to_char(j, '9999'), 12)||lpad(to_char(total, '9.9EEEE'), 15)
end;
return next;
end;
end loop;
end;
$body$;
Invoke it like this:
\t on
select t from total_paths_versus_number_of_nodes(20);
\t off
This is the result:
no. of nodes no. of paths
------------ ------------
4 15
5 64
6 325
7 1,956
8 13,699
9 109,600
10 986,409
11 9,864,100
12 1.1e+08
13 1.3e+09
14 1.7e+10
15 2.4e+11
16 3.6e+12
17 5.7e+13
18 9.7e+14
19 1.7e+16
20 3.3e+17
The growth rate is astonishing. You can see immediately that there must be a limit to the viability of using a "find_paths()" implementation that doesn't do early path pruning as the size of the maximally connected graph increases. The following thought experiment makes this clear.
Suppose that a clever, highly compressive, representation scheme were invented to store paths with an average space consumption per path of, say, just 10 bytes. And suppose that you invest in a 1 TB external SSD drive for your laptop to hold paths represented using this clever scheme. Your SSD's capacity is 2^40 bytes—about 10^12 bytes. This isn't enough to store the 2.4*10^11 paths that a maximally connected graph with just 15 nodes has.
Consider trying this test again and again with increasing values for :nr_nodes.
-- Sketch of stress-test kernel.
delete from edges;
call populate_maximum_connectvity_edges(nr_nodes=>:nr_nodes);
insert into edges(node_1, node_2)
select node_2 as node_1, node_1 as node_2
from edges;
call find_paths(start_node => 'n001', prune => false);
Even if you did create a single-node YugabyteDB cluster so that it used your 1 TB SSD for its data files, you doubtless wouldn't have the capacity for the paths for even a 14-node maximally connected graph because the hypothetical dedicated highly compressive path representation scheme isn't in use. This can only mean that the "find_paths()" execution would crash for some run with fewer nodes than 14.
The stress test experiment
The thought experiment, above, was described to show that the "find_paths()" scheme that uses schema-level tables to implement the intermediate and final results for the recursive CTE algorithm, without pruning, will inevitably reach a limit and crash when the target graph has too many paths. Similar reasoning shows that the ordinary, explicit, use of the recursive CTE will inevitably crash, too, under similar circumstances. There's no point in trying to make more realistic estimates of the various sizes that will jointly conspire to bring eventual failure. Rather, an empirical test better serves the purpose.
Before doing the stress-test experiment, make sure that you have created the "edges" table (see cr-edges.sql) and installed all the code shown in the section Common code for traversing all kinds of graph. But this time, make sure that you start by choosing the option that re-creates the "raw_paths" table without the tracing code before you do some timing tests.)
Note: The stress-test is implemented by a few scripts where all but one call other script(s). In order to run the whole test, you should create a directory on your computer and, when told to, save each script there with the name that's given. The downloadable code zip arranges all of the scripts it includes in a directory tree that implements a useful classification scheme. This means that, in the files from the zip, the arguments of the \i, \ir, and \o meta-commands are spelled differently than they are here to include directory names.
Create some helpers
A scripting scheme is needed to call the basic test (see the code, above, that starts with the comment "Sketch of stress-test kernel") repeatedly for each value of interest of :nr_nodes and after installing, in turn, each of the three methods. It will also be useful if the stress-test kernel times each invocation of "find_paths()".
The "find_paths()" invocation syntax depends on the present method. A procedure manages this nicely:
cr-invoke-find-paths.sql
drop procedure if exists invoke_find_paths(text) cascade;
create procedure invoke_find_paths(method in text)
language plpgsql
as $body$
begin
case method
when 'pure-with' then call find_paths(start_node => 'n001');
when 'prune-false' then call find_paths(start_node => 'n001', prune => false);
when 'prune-true' then call find_paths(start_node => 'n001', prune => true);
end case;
end;
$body$;
The stress-test kernel must spool the output to a file whose name encodes the present number of nodes and method name. A well-known pattern comes to the rescue: use a table function to write the script that turns on spooling and invoke that script. This is the function:
cr-start-spooling-script.sql
drop function if exists start_spooling_script(int, text) cascade;
create function start_spooling_script(nr_nodes in int, method in text)
returns text
language plpgsql
as $body$
begin
return '\o '||ltrim(nr_nodes::text)||'-nodes--'||method||'.txt';
end;
$body$;
Create a script to do the stress-test kernel
With the two building blocks, the procedure "invoke_find_paths()" and the function "start_spooling_script()", in place, the following script implements the stress-test kernel:
do-stress-test-kernel.sql
Save this script.
delete from edges;
call populate_maximum_connectvity_edges(nr_nodes=>:nr_nodes);
-- Implement the denormalization.
insert into edges(node_1, node_2)
select node_2 as node_1, node_1 as node_2
from edges;
\t on
\o start_spooling.sql
select start_spooling_script(:nr_nodes, :method);
\o
\i start_spooling.sql
select :method||' -- '||ltrim(:nr_nodes::text)||' nodes';
call start_stopwatch();
call invoke_find_paths(:method);
select 'elapsed time: '||stopwatch_reading() as t;
select 'count(*) from raw_paths: '||ltrim(to_char(count(*), '9,999,999')) from raw_paths;
\o
\t off
You can manually test a single use of it. First decide on the method. These are the choices:
-
"pure-with" —
cr-find-paths-with-nocycle-check.sql -
"prune-false" —
cr-find-paths-with-pruning.sqlinvoked withprune => false -
"prune-true" —
cr-find-paths-with-pruning.sqlinvoked withprune => true
Decide on the number of nodes, for example 7. And choose the method, for example "pure-with". (Remember to install it.) Then do this:
\set nr_nodes 7
\set method '\''prune-false'\''
\i do-stress-test-kernel.sql
This will produce the 7-nodes--prune-false.txt spool file. It will look like this:
prune-false -- 7 nodes
elapsed time: 40 ms.
count(*) from raw_paths: 1,956
Of course, the reported elapsed time that you see will doubtless differ from "40 ms".
Implement scripts to execute the stress-test kernel for each method for each of the numbers of nodes in the range of interest
First, implement a script to invoke each of the three methods for a particular, pre-set, value of :nr_nodes. Get a clean slate for the "paths" tables before each timing test by dropping and re-creating each of them.
do-stress-test-for-all-methods.sql
Save this script. You'll also need to save the scripts that it calls: cr-raw-paths-no-tracing.sql, cr-supporting-path-tables.sql, cr-find-paths-with-nocycle-check.sql, and cr-find-paths-with-pruning.sql.
\set method '\''pure-with'\''
\i cr-raw-paths-no-tracing.sql
\i cr-supporting-path-tables.sql
\i cr-find-paths-with-nocycle-check.sql
\i do-stress-test-kernel.sql
\set method '\''prune-false'\''
\i cr-raw-paths-no-tracing.sql
\i cr-supporting-path-tables.sql
\i cr-find-paths-with-pruning.sql
\i do-stress-test-kernel.sql
\set method '\''prune-true'\''
\i cr-raw-paths-no-tracing.sql
\i cr-supporting-path-tables.sql
\i cr-find-paths-with-pruning.sql
\i do-stress-test-kernel.sql
Finally, create a script to invoke do-stress-test-for-all-methods.sql for each of the numbers of nodes in the range of interest.
do-stress-test.sql
Save this script.
\set nr_nodes 4
\i do-stress-test-for-all-methods.sql
\set nr_nodes 5
\i do-stress-test-for-all-methods.sql
\set nr_nodes 6
\i do-stress-test-for-all-methods.sql
\set nr_nodes 7
\i do-stress-test-for-all-methods.sql
\set nr_nodes 8
\i do-stress-test-for-all-methods.sql
\set nr_nodes 9
\i do-stress-test-for-all-methods.sql
\set nr_nodes 10
\i do-stress-test-for-all-methods.sql
Then invoke do-stress-test-kernel.sql by hand for each of the three methods, setting the number of nodes to 11. You'll see that each of "pure-with" and "prune-false" fails, with error messages that reflect the fact that the implementation can't handle as many as 9,864,100 nodes. But "prune-true" completes without error very quickly.
Finally, invoke do-stress-test-kernel.sql by hand using the "prune-true" method and 100 nodes. You'll see that it completes without error in about the same time as for any smaller number of nodes.
Here are the results:
The elapsed times are in seconds.
| no. of nodes | no. of paths | pure-with | prune-false | prune-true |
|---|---|---|---|---|
| 4 | 15 | 0.1 | 0.1 | 0.2 |
| 5 | 64 | 0.1 | 0.1 | 0.2 |
| 6 | 325 | 0.1 | 0.2 | 0.2 |
| 7 | 1,956 | 0.2 | 0.7 | 0.2 |
| 8 | 13,699 | 0.5 | 3.8 | 0.2 |
| 9 | 109,600 | 4.1 | 31.3 | 0.2 |
| 10 | 986,409 | 42.51 | 297.01 | 0.2 |
| 11 | 9,864,100 | crash [1] | crash [2] | 0.2 |
| 100 | 2.5e+156 | 0.3 |
[1] Failed after 12 min. "Timed out: Read RPC (request call id 42549) to 127.0.0.1:9100 timed out after 1.117s"
[2] Failed after 48:52 min.with errors like this: "Timed out: Read RPC (request call id 9911242) to 127.0.0.1:9100 timed out after 0.983s."
The experiment shows that the "prune-false" approach is never preferable to the "pure-with" approach. Each fails beyond a 10-node graph; and the "prune-false" method is slower. This is very much to be expected. It was implemented only for pedagogic purposes and, more importantly, to provide the framework that allows the implementation of early pruning—the "prune-true" approach.
The experiment also shows that the "prune-true" approach is viable and quick even for graphs with unimaginably huge numbers of possible paths.
This leads to two conclusions:
-
It simply isn't feasible to use the native recursive CTE features of YugabyteDB, those of PostgreSQL, or indeed those of any SQL database, to discover all the paths in any typically highly connected graph that's likely to be interesting in practice—especially, for example, the IMDb data.
-
It is straightforward to use ordinary SQL and stored procedure features to discover the shortest paths in even very large and highly connected graphs. As noted, you cannot use the recursive CTE for this purpose because it doesn't let you implement early pruning. Rather, you must use a table-based approach that implements the recursive CTE's algorithm explicitly by hand.
Implication of the stress-test experiment for the implementation of the computation of Bacon Numbers
The introduction to the section Using a recursive CTE to compute Bacon Numbers for actors listed in the IMDb mentions this data set:
- imdb.small.txt: a... file with just a handful of performers (161), fully connected
It seems very likely that a fully connected undirected cyclic graph with 161 nodes, even if it isn't maximally connected will be highly connected—very many of the nodes will have edges to very many of the other nodes. It's therefore likely that the implementation of the computation of Bacon Numbers will have to use the "prune-true" approach.