Case study: using a recursive CTE to compute Bacon Numbers for actors listed in the IMDb
The Bacon Numbers problem, sometimes referred to as "The Six_Degrees of Kevin Bacon" (see this Wikipedia article), is a specific formulation of the general problem of tracing paths in an undirected cyclic graph. It is a well-known set-piece exercise in graph analysis and is a popular assignment task in computer science courses. Most frequently, solutions are implemented in an "if-then-else" language like Java. Interestingly, solutions can be implemented in SQL and, as this section will show, the amount of SQL needed is remarkably small.
Representing actors and movies data
The Bacon Numbers problem is conventionally formulated in the context of the data represented in the IMDb—an acronym for Internet Movie Database. See this Wikipedia article. The data are freely available from IMDb but it's better, for the purposes of this section's pedagogy, to use sufficient subsets of the total IMDb content. These subsets restrict the population to the movies in which Kevin Bacon has acted and project the facts about the actors and movies to just their names. This entity relationship diagram (a.k.a. ERD) depicts the sufficient subset of the IMDb:
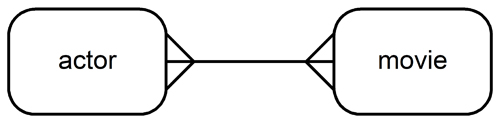
- each actor must act in at least one movie
- each movie's cast must list at least one actor
The actors are the nodes in an undirected cyclic graph. There is an edge between two actors when they both have acted together in at least one movie.
The ERD implies the conventional three-table representation with an "actors table, a "movies_table", and a "cast_members" intersection table. Create them with this script:
cr-actors-movies-cast-members-tables.sql
drop table if exists actors cascade;
drop table if exists movies cascade;
drop table if exists cast_members cascade;
create table actors(
actor text primary key);
create table movies(movie text primary key);
create table cast_members(
actor text not null,
movie text not null,
constraint cast_members_pk primary key(actor, movie),
constraint cast_members_fk1 foreign key(actor)
references actors(actor)
match full
on delete cascade
on update restrict,
constraint cast_members_fk2 foreign key(movie)
references movies(movie)
match full
on delete cascade
on update restrict
);
Of course, the IMDb has facts like date of birth, nationality, and so on for the actors and like release date, language and so on for the movies. The information would doubtless allow the "cast_members" table to have columns like "character_name". The data that this case study uses happen to include the movie release date, in parentheses, after the movie name in a single text field. The pedagogy is sufficiently served without parsing out these two facts into separate columns in the "movies" table.
Notice that the notion of a graph is so far only implied. A derived "edges" table makes the graph explicit. An edge exists between a pair of actors if they are both on the cast list of the same one or more movies. The SQL needed to populate the "edges" table from the "cast_members" table is straightforward.
When the paths have been found, it's useful to be able to annotate each edge with the list of movies that are responsible for its existence. The annotation code could, of course, derive this information dynamically. But it simplifies the overall coding scheme if a denormalization is adopted to annotate the paths at the time that they are discovered. Another departure from strict purity simplifies the overall coding scheme further. If the row for the edge between a particular pair of actors records the list of movies that brought it (rather than recording many edges, each with a single-valued "movie" attribute), then the path-tracing code that the section Using a recursive CTE to traverse graphs of all kinds presented can be used "as is". To this end, the columns that represent the actor pair in the "edges" table are called "node_1" and "node_2" rather than the more natural "actor_1" and "actor_2".
Note: The previous paragraph was stated as something of a sketch. In fact, each edge between a pair of actors is recorded twice—once in each direction, as is described in the section Graph traversal using the denormalized "edges" table design. Each of the edges in such a pair is annotated with the same list of movies.
This code creates the "edges" table and the procedure that populates it.
cr-actors-movies-edges-table-and-proc.sql
drop table if exists edges cascade;
create table edges(
node_1 text,
node_2 text,
movies text[],
constraint edges_pk primary key(node_1, node_2),
constraint edges_fk_1 foreign key(node_1) references actors(actor),
constraint edges_fk_2 foreign key(node_2) references actors(actor));
drop procedure if exists insert_edges() cascade;
create or replace procedure insert_edges()
language plpgsql
as $body$
begin
delete from edges;
with
v1(node_1, movie) as (
select actor, movie from cast_members),
v2(node_2, movie) as (
select actor, movie from cast_members)
insert into edges(node_1, node_2, movies)
select node_1, node_2, array_agg(movie order by movie)
from v1 inner join v2 using (movie)
where node_1 < node_2
group by node_1, node_2;
insert into edges(node_1, node_2, movies)
select node_2 as node_1, node_1 as node_2, movies
from edges;
end;
$body$;
Notice the second INSERT statement that re-inserts all the discovered directed edges in the reverse direction. The value of this denormalization is explained in the section Finding the paths in a general undirected cyclic graph.
Create a stored procedure to decorate path edges with the list of movies that brought each edge
The stored procedure (actually a table function) will annotate each successive edge along each path in the specified table with the list of movies that brought that edge.
-
When there are relatively few paths in all, as there are with the synthetic data that the section Computing Bacon Numbers for a small set of synthetic actors and movies data uses, it's convenient simply to show all the decorated paths.
-
However, with a data set as big as the IMDb (even the imdb.small.txt subset has 160 shortest paths), it's useful to be able to name a candidate actor and to annotate just the shortest path (more carefully stated, one of the shortest paths) from Kevin Bacon to the candidate. The site The Oracle of Bacon exposes this functionality.
The first formal parameter of the function "decorated_paths_report()" is mandatory and specifies the table in which the paths are represented. The second optional formal parameter, "terminal", lets you specify the last node along a path. If you omit it, the meaning is "report all the paths"; and it you supply it, the meaning is "report the path to the specified actor".
Dynamic SQL is therefore needed for two reasons, each of which alone is a sufficient reason:
-
The table name isn't known until run-time.
-
There may, or may not, be a
WHEREclause.
cr-decorated-paths-report.sql
drop function if exists decorated_paths_report(text, text) cascade;
-- This procedure is more elaborate than you'd expect because of GitHub Issue 3286.
-- It says this in the report:
--
-- Commit 9d66392 added support for cursor. Our next releases will have this work.
-- However, there are a few pending issues.
--
-- Meanwhile, this code works around the issue by using a single-row SELECT... INTO.
-- This is made possible by using array_agg(). But you cannot aggregate arrays of
-- different cardinalities. So a second-level workaround is used. Each array in
-- the result set is cast to "text" for aggregation and then cast back to the array
-- that it represents in the body of the FOREACH loop that steps through the text
-- values that have been aggregated.
--
-- When a "stable" release supports the use of a cursor variable, this implementation
-- will be replaced by a more straightforward version.
create function decorated_paths_report(tab in text, terminal in text default null)
returns table(t text)
language plpgsql
as $body$
<<b>>declare
indent constant int := 3;
q constant text := '''';
stmt_start constant text := 'select array_agg((path::text) '||
'order by cardinality(path), terminal(path), path) '||
'from ?';
where_ constant text := ' where terminal(path) = $1';
all_terminals_stmt constant text := replace(stmt_start, '?', tab);
one_terminal_stmt constant text := replace(stmt_start, '?', tab)||where_;
paths text[] not null := '{}';
p text not null := '';
path text[] not null := '{}';
distance int not null := -1;
match text not null := '';
prev_match text not null := '';
movies text[] not null := '{}';
movie text not null := '';
pad int not null := 0;
begin
case terminal is null
when true then
execute all_terminals_stmt into paths;
else
execute one_terminal_stmt into paths using terminal;
end case;
foreach p in array paths loop
path := p::text[];
distance := cardinality(path) - 1;
match := terminal(path);
-- Rule off before each new match.
case match = prev_match
when false then
t := rpad('-', 50, '-'); return next;
end case;
prev_match := match;
pad := 0;
t := rpad(' ', pad)||path[1]; return next;
<<step_loop>>
for j in 2..cardinality(path) loop
select e.movies
into strict b.movies
from edges e
where e.node_1 = path[j - 1] and e.node_2 = path[j];
pad := pad + indent;
<<movies_loop>>
foreach movie in array movies loop
t := rpad(' ', pad)||movie::text; return next;
end loop movies_loop;
pad := pad + indent;
t := rpad(' ', pad)||path[j]; return next;
end loop step_loop;
end loop;
t := rpad('-', 50, '-'); return next;
end b;
$body$;
Computing Bacon Numbers for synthetic data and the real IMDb data
The section Computing Bacon Numbers for a small set of synthetic actors and movies data demonstrates the approach using a small data set.
The section Computing Bacon Numbers for real IMDb data shows how to ingest the raw imdb.small.txt file into the same representation that was used for the synthetic data. (The subsection Download and ingest some IMDb data explains how to download the IMDb subset that this case study uses.)
While a straightforward use of a recursive CTE can be used to produce the solution for the small synthetic data set quickly, it fails to complete before crashing (see the section Stress testing different find_paths() implementations on maximally connected graphs) when it's applied to the ingested imdb.small.txt data. The approach described in the How to implement early path pruning section comes to the rescue.