Using a recursive CTE to traverse graphs of all kinds
Download the code examples
All of the .sql scripts that this section presents for copy-and-paste at the ysqlsh prompt are included for download in a zip-file.
Download recursive-cte-code-examples.zip.
After unzipping it on a convenient new directory, you'll see a README.txt. It tells you how to start a couple of master-scripts. Simply start each in ysqlsh. You can run them time and again. They always finish silently. You can see the reports that they produce on dedicated spool directories and confirm that your reports are identical to the reference copies that are delivered in the zip-file.
A graph is a network of nodes (sometimes called vertices) and edges (sometimes called arcs). An edge joins a pair of nodes.
- When every edge is undirected (i.e. the relationship between the nodes at each end of an edge is symmetrical), then the graph is called an undirected graph.
- When every edge is directed, then the graph is called a directed graph.
- One representation scheme for an undirected edge chooses to represent this single abstract edge as two physical edges, one in each direction. In this sense, you can think of a general undirected graph as a directed graph where at least one pair of nodes is connected by a pair of edges, one in each direction. By extension of this thinking, a directed graph is one where there is maximum one directed edge between any pair of nodes.
- Most commonly (by virtue of the nature of the inter-node relationship) a graph has either only undirected edges or only directed edges.
- A path is a traversal of the graph that starts at one node, goes along an edge to another node, and then along an edge to yet another node, and so on. You can certainly give meaning to a path that returns many times to nodes that have already been encountered. This is called a cycle. But, by convention, this is not done because an algorithm that discovered such a path would run for ever. Rather, it's usual that the definition of a path includes the notion that it has no cycles, so that no node is visited more than once. (A cycle that runs round and round between a pair of immediately connected nodes is always discounted.)
- A graph that has the potential for cycles is called a cyclic graph. And one with no such potential is called an acyclic graph.
- The two degrees of freedom, undirected or directed and cyclic or acyclic are orthogonal—i.e. all four combinations are possible.
- The most general kind of graph is undirected and cyclic and the design of the traversal scheme must account for this. This general scheme will always work on the more specialized kinds of graph.
- A graph might be just a single set of connected nodes, where every node can be reached from any other node; or it might be two or more isolated subgraphs of mutually connected nodes where there exists no path between any pair of subgraphs.
- The most general graph traversal scheme, therefore, must discover all the isolated subgraphs and apply the required traversal scheme to each of them. This is beyond the scope of this overall section. It deals only with single connected graphs.
You can use a recursive CTE to find the paths in an undirected cyclic graph. But you must design the SQL explicitly to accommodate the fact that the edges are undirected and you must include an explicit predicate to prevent cycles. Because each other kind of graph described below is a specialization of the graph whose description immediately precedes its description, you can, as mentioned, use progressively simpler SQL to trace paths in these—as long as you know, a priori, what kind of graph you're dealing with.
Undirected cyclic graph
Here is an example of such a graph.
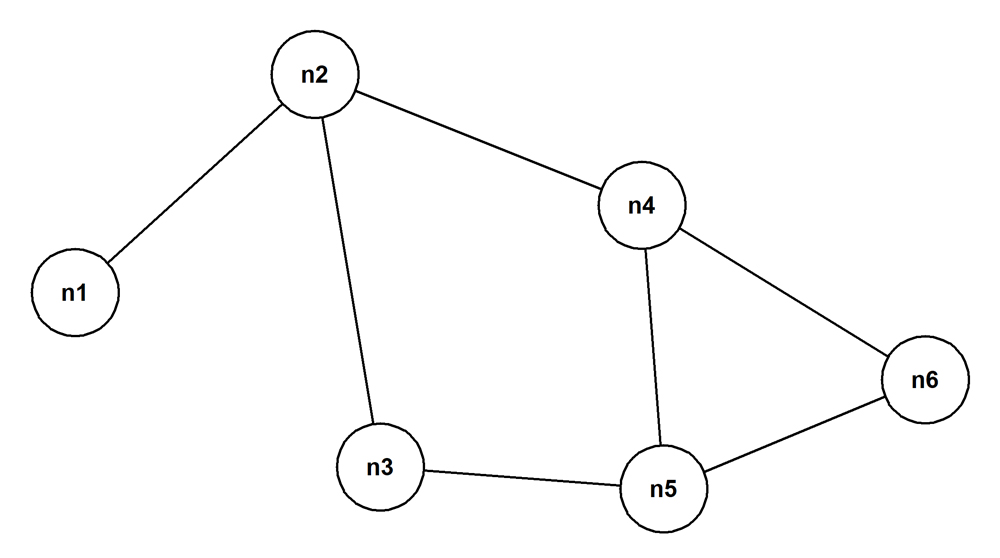
The Bacon Numbers problem is specified in the context of this kind of graph. Actors have acted in one or more movies. And the cast of a movie is one or more actors. The set of actors of interest is represented as the nodes of a single connected graph, one of whose nodes is Kevin Bacon. When any pair of actors have acted in the same movie, an edge exist between the two of them.
-
Setting aside notions like "starring role", "supporting role", and so on, the relationship between a pair of actors who acted in the same movie is symmetrical. So the graph is undirected.
-
Because, for example, John Malkovich, Brad Pitt, and Winona Ryder all acted in the 1999 movie "Being John Malkovich", you could traverse a path from John Malkovich to Brad Pitt to Winona Ryder and back to John Malkovich, and so on indefinitely. Or you could traverse a path from John Malkovich to Winona Ryder to Brad Pitt and back to John Malkovich, and so on indefinitely. So the graph, in general, is undirected and cyclic.
The movies-and-actors use case brings out another point. In general, the edges have properties—in this case the list of movies in which a particular pair of actors have both acted.
You might argue (particularly if you're starting to think of a representation in a SQL database) that the properties of an edge must be single-valued and that there should therefore be many edges between a pair of actors who've been in several movies in common—one for each movie. This is just an example of the usual distinction between the conceptual design (the entity-relationship model) and the logical design (the table model). The basic graph traversal problem is, beyond doubt, best conceptualized in terms of a model that allows just zero or one edge between node pairs. Even so, the traversal implementation can easily accommodate a physical model that allows more than one edge between node pairs.
Directed cyclic graph
A directed cyclic graph is a specialization of the undirected cyclic graph. Here, the relationship between the nodes at the two ends of an edge is asymmetrical, so each edge has a direction.
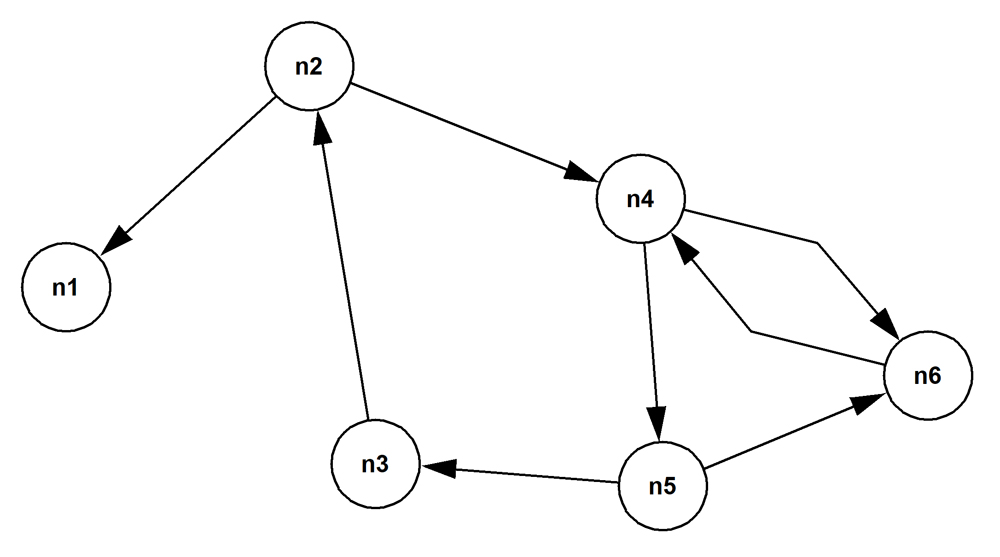
For example, you might keep a record of all the video-conferences that are held among the employees in an organization. A conference has exactly one host attendee and one or many invited attendees. Alice might host several conferences at which Joe attends as an invitee. And Joe might host several conferences at which Alice attends as an invitee. The graph will therefor have two directed edges between Alice and Joe (as is shown between the nodes n4 and n6 in the picture above). The property of the edge from Alice to Joe could include the list of start timestamps and durations of the conferences that Alice hosted and that Joe attended. And the property of edge from Joe to Alice would then include the list of start timestamps and durations of the conferences that Joe hosted and that Alice attended.
Directed acyclic graph
A directed acyclic graph is a specialization of the directed cyclic graph.
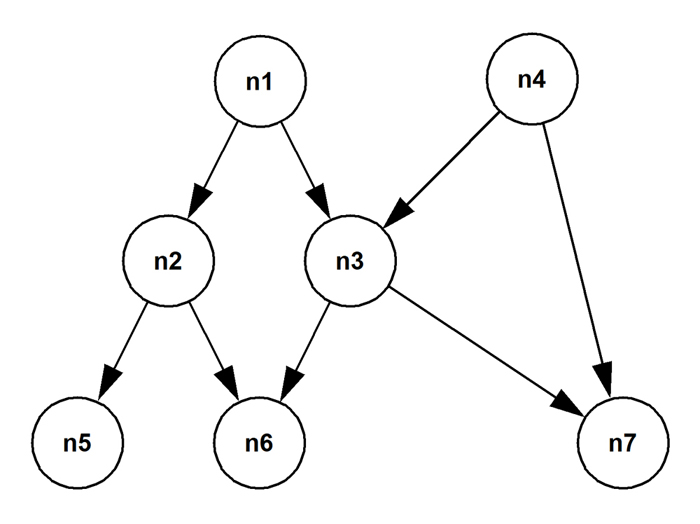
A car manufacturer will record the parts decomposition of each model that it makes. Cars have major components like engines, brakes, exhaust systems, and so on. And many car models (especially, for example, the sedan and wagon variants of a particular marque) will share the same major components. The relationship "is composed of" is clearly asymmetrical. Major components, of course, have their own parts breakdowns into subcomponents, as do the subcomponents in turn all the way down to atomic subcomponents like nuts, bolts, washers, and so on.
Rooted tree
A rooted tree is a specialization of the directed acyclic graph.
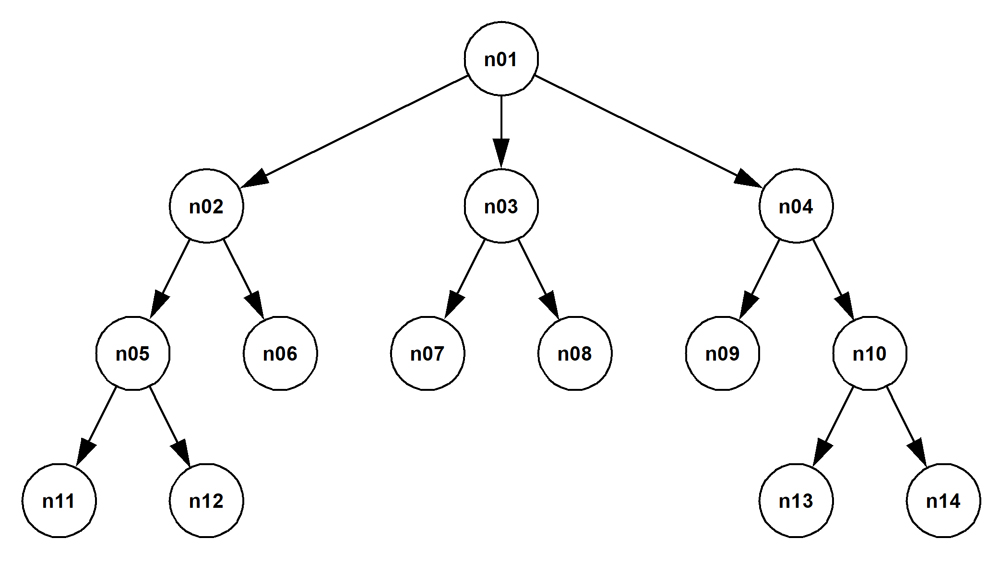
The reporting tree for employees in an organization, whose traversal was discussed in the section Case study—Using a recursive CTE to traverse an employee hierarchy is the canonical example of such a graph.
Finding the paths in each of the four kinds of graph
The next sections show how to find the paths in each of the four kinds of graph that are described above.
Representing the different kinds of graph in a SQL database
This section describes the minimal table structure for representing graphs.
Common code for traversing all kinds of graph
This section describes common artifacts, like tables into which to insert the results to support subsequent ad hoc queries, and various helper functions and procedures, upon which the described traversal schemes all depend.
Path finding approaches
The method for the directed cyclic graph is identical to that for the undirected cyclic graph. Each implements cycle prevention. But the table for the directed cyclic graph usually records just the edge as either "from a to b" or "from b to a". Using the recommended representation for edges in a SQL database table, this is the difference:
-
The table for the undirected cyclic graph for the edge between nodes "a" and "b" records it twice, as "from a to b" and "from b to a".
-
But the table for the directed cyclic graph usually records just the edge as either "from a to b" or "from b to a". Occasionally, when the directed relationship between a particular pair of nodes is reciprocal, two edges will be recorded as "from a to b" and "from b to a".
The method for the directed acyclic graph is identical to that for the rooted tree. Neither implements cycle prevention because there is no need for this (both these kinds of graph, by definition, have no cycles). For the same reason, there is never more than one directed edge between any pair of nodes.
The methods are described in these sections: