Finding the paths in a general undirected cyclic graph
Before trying any of the code in this section, make sure that you have created the "edges" table (see cr-edges.sql) and installed all the code shown in the section Common code for traversing all kinds of graph.
Graph traversal using the denormalized "edges" table design
Start by populating the "edges" table with the data that defines the graph shown in the section Undirected cyclic graph using the scheme that represents each undirected edge twice—once in each direction.
delete from edges;
alter table edges drop constraint if exists edges_chk cascade;
alter table edges add constraint edges_chk check(node_1 <> node_2);
insert into edges(node_1, node_2) values
('n1', 'n2'),
('n2', 'n3'),
('n2', 'n4'),
('n3', 'n5'),
('n4', 'n5'),
('n4', 'n6'),
('n5', 'n6');
-- Implement the denormalization.
insert into edges(node_1, node_2)
select node_2 as node_1, node_1 as node_2
from edges;
Look back at the SQL for traversing an employee hierarchy (see the section List the path top-down from the ultimate manager to each employee in breadth first order). The snippet here is the core algorithm. But it's re-written to transform it into a use-case agnostic form by making these substitutions:
emps > nodes
[the alias] e > n
emps.name > nodes.node_id
emps.mgr_name > nodes.parent_node_id
This is the code that results:
with
recursive paths(path) as (
select array[node_id]
from nodes
where parent_node_id is null
union all
select p.path||n.node_id
from nodes as n
inner join paths as p on n.parent_node_id = p.path[cardinality(path)]
)
select path from paths
The first attempt at the SQL for traversing the present undirected cyclic graph is easily written down just as an obvious paraphrase:
deallocate all;
prepare stmt(text) as
with
recursive paths(path) as (
select array[$1, node_2]
from edges
where node_1 = $1
union all
select p.path||e.node_2
from edges e
inner join paths p on e.node_1 = terminal(p.path)
)
select path from paths;
Notice what the changes are.
-
The hierarchy's "nodes" table is replaced by the general graph's "edges" table.
-
The hierarchy's "parent_node_id" column is replaced by the general graph's "node_1" column. Similarly, the hierarchy's "node_id", is replaced by the general graph's "node_2".
-
The fixed starting condition for the hierarchy in the non-recursive term (
parent_node_id is null) is replaced by the parameterized choice of start node for the general graph (node_1 = $1). And this implies replacing theSELECTlist'sarray[]value constructor (array[node_id]) witharray[$1, node_2]. -
The stopping condition in the hierarchy's recursive term (
n.parent_node_id = p.path[cardinality(path)]) is replaced withnode_1 = terminal(p.path)-- but this is only a cosmetic change because the function "terminal()" is just a wrapper for the final element in the path. -
And the
SELECTlist'sarray[]value constructor in the non-recursive term gets changed appropriately.
Now execute it:
execute stmt ('n1');
Though the statement compiled without error, and seems to be executing, it will never stop. You must interrupt it with ctrl-C. The reason, of course, is that the traversal reached one of the cycles (either "n2→n3→n5→n4→n2..." or "n2→n4→n5→n3→n2...") and will go around it time and again indefinitely. Extra SQL is needed to preempt this problem.
Notice that the next node along the path that is so-far defined by the row that the WHERE predicate tests for accumulation into the growing results set under the present repetition of the recursive term, and that would begin the unending cycle, might be anywhere along the present path, according to the graph's topology. The ANY test comes to the rescue. Try this:
select ('n3' = any (array['n1', 'n2', 'n3', 'n5', 'n4']::text[]))::text as "cycle starting";
This is the result:
cycle starting
----------------
true
It's easy to add this predicate to the recursive CTE (in its recursive term). It's convenient to encapsulate the cycle-proof SQL in a "language plpgsql" procedure so that the identity of the start node can be named usefully. It's also useful to record the result in a table to allow trying various ad hoc analysis queries after the fact.
cr-find-paths-with-nocycle-check.sql
drop procedure if exists find_paths(text) cascade;
create procedure find_paths(start_node in text)
language plpgsql
as $body$
begin
-- See "cr-find-paths-with-pruning.sql". This index demonstrates that
-- no more than one path has been found to any particular terminal node.
drop index if exists raw_paths_terminal_unq cascade;
commit;
delete from raw_paths;
with
recursive paths(path) as (
select array[start_node, node_2]
from edges
where node_1 = start_node
union all
select p.path||e.node_2
from edges e
inner join paths p on e.node_1 = terminal(p.path)
where not e.node_2 = any(p.path) -- <<<<< Prevent cycles.
)
insert into raw_paths(path)
select path
from paths;
end;
$body$;
Invoke it and the use the "list_paths()" table function show the result thus:
call find_paths(start_node => 'n1');
\t on
select t from list_paths('raw_paths');
\t off
This is the result:
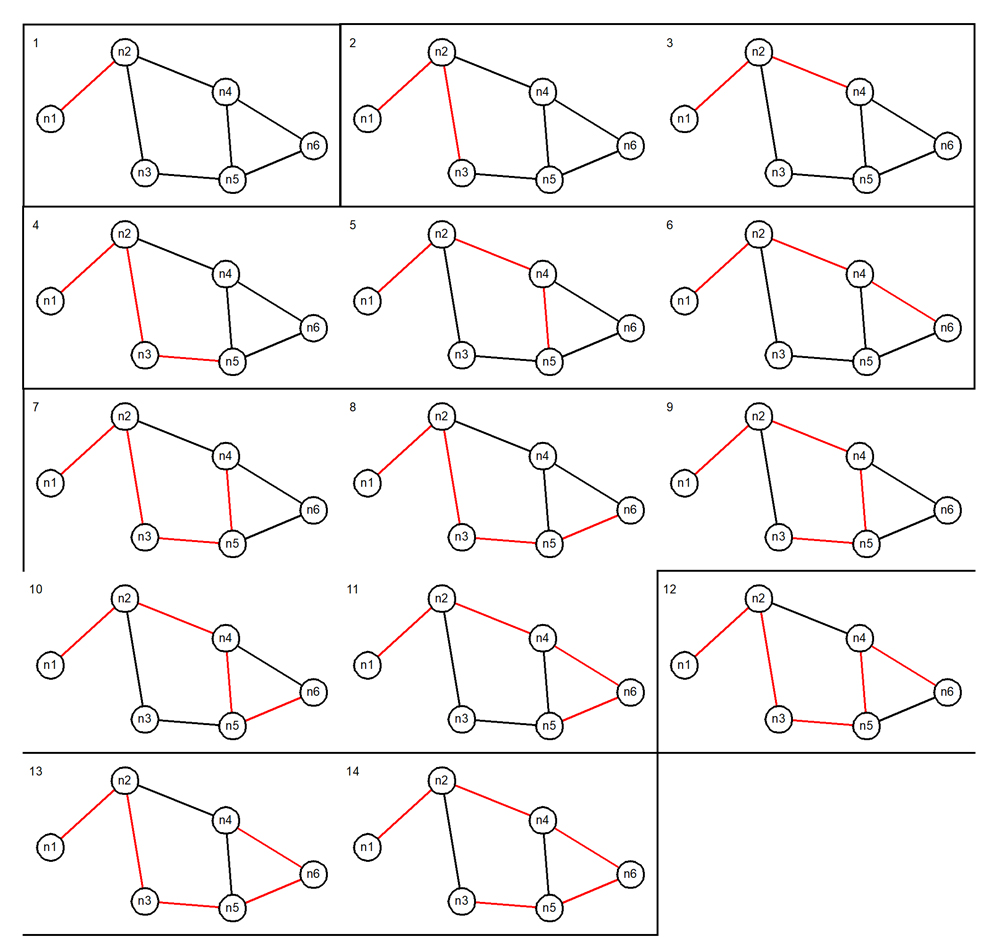
path # cardinality path
------ ----------- ----
1 2 n1 > n2
2 3 n1 > n2 > n3
3 3 n1 > n2 > n4
4 4 n1 > n2 > n3 > n5
5 4 n1 > n2 > n4 > n5
6 4 n1 > n2 > n4 > n6
7 5 n1 > n2 > n3 > n5 > n4
8 5 n1 > n2 > n3 > n5 > n6
9 5 n1 > n2 > n4 > n5 > n3
10 5 n1 > n2 > n4 > n5 > n6
11 5 n1 > n2 > n4 > n6 > n5
12 6 n1 > n2 > n3 > n5 > n4 > n6
13 6 n1 > n2 > n3 > n5 > n6 > n4
14 6 n1 > n2 > n4 > n6 > n5 > n3
The whitespace was added manually to separate the paths into groups of the same cardinality to improve readability. The index on the "path" column confirms that each of the fourteen paths is unique. Here they are. The pictures are numbered with the value assigned by row_number() (see the implementation of "list_paths()") and the cardinality groups are distinguished by boxing in each group.
Restrict down to a single shortest path to each distinct node reached from the start node
As explained in the section Create a procedure to filter the paths from "raw_paths" to leave only a shortest path to each distinct terminal node, the Bacon Numbers problem requires only that (one of the) the shortest path(s) from one node to every other node is found. The following approach produces the required paths after the fact on the table of all paths.
Use the "restrict_to_shortest_paths()" procedure to derive these paths and then show them:
call restrict_to_shortest_paths('raw_paths', 'shortest_paths');
\t on
select t from list_paths('shortest_paths');
\t off
Note: As will be shown in the section Produce the sets of shortest paths starting from every node, it is interesting to accumulate the sets of shortest paths from each of many nodes into the "shortest_paths" table. This is why the choice to purge the table before calling "restrict_to_shortest_paths()" is left to the user. In contrast, the "find_paths()" procedure starts by deleting all rows that the target "raw_paths" table might contain. This is a design choice. If it simply accumulated paths from each successive call (invoking each of these with a different actual value for the "start_node" formal parameter), then there'd be no errors. But the logic of the "restrict_to_shortest_paths()" procedure would need to be more elaborate than the version that's presented here that expects to find only paths all of which have the same starting note. This would have made the essential core logic harder for you to understand.
Here is the result:
path # cardinality path
------ ----------- ----
1 2 n1 > n2
2 3 n1 > n2 > n3
3 3 n1 > n2 > n4
4 4 n1 > n2 > n3 > n5
5 4 n1 > n2 > n4 > n6
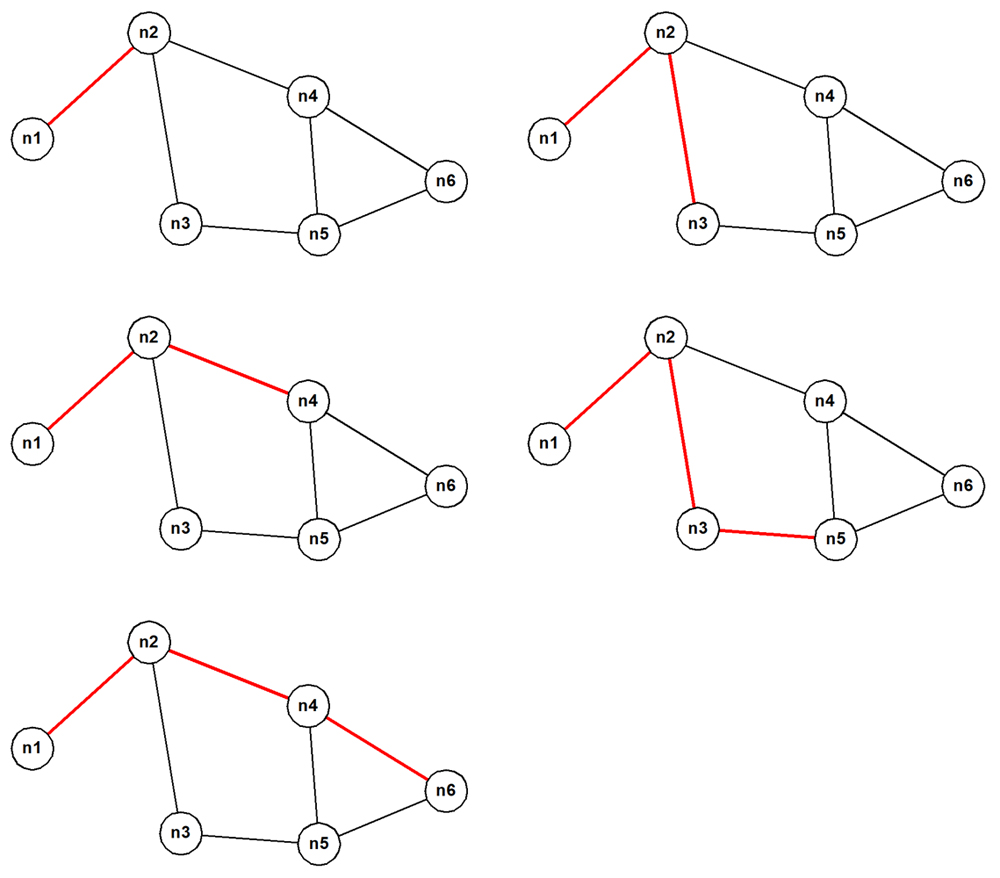
Pruning after the fact in this way is a useful pedagogic device in that it clearly shows what information is sufficient to solve the Bacon Numbers problem. However, pairs of actor nodes that are defined by the real IMDb data have huge numbers of connecting paths with a wide range of lengths because so many movies share the same subsets of many actors. This means that when the approach that this section has explained is run on this kind of data, it takes a very long time to run and consumes a huge amount of memory for the ever-growing representation of the eventual result set. (There is no mechanism for spilling to disk.) The outcome is either that the query fails to finish in reasonable time or that it simply crashes with an "out of resources" error of some kind.
The remedy is obvious: at each repeat of the recursive term, compare the new about-to-be-accumulated rows with the entire set of already-accumulated rows and discard all new rows whose end node is the same as that of an already-found shorter path. It turns out that the constructs available to the SQL programmer of a recursive CTE don't support this early pruning and so an approach must be designed that does allow this. This is the focus of the section How to implement early path pruning.
Produce the sets of shortest paths starting from every node
Do this to produce, in turn, all of the paths starting from each remaining node (i.e. apart from "n1") and then to accumulate the output of "restrict_to_shortest_paths()" into the "shortest_paths" table:
do $body$
declare
node text not null := '';
begin
for node in (
select distinct node_1 from edges
where node_1 <> 'n1')
loop
call find_paths(start_node => node);
call restrict_to_shortest_paths('raw_paths', 'shortest_paths', append=>true);
end loop;
end;
$body$;
Now show the result:
\t on
select t from list_paths('shortest_paths');
\t off
This is the result:
path # cardinality path
------ ----------- ----
1 2 n1 > n2
2 3 n1 > n2 > n3
3 3 n1 > n2 > n4
4 4 n1 > n2 > n3 > n5
5 4 n1 > n2 > n4 > n6
6 2 n2 > n1
7 2 n2 > n3
8 2 n2 > n4
9 3 n2 > n3 > n5
10 3 n2 > n4 > n6
11 2 n3 > n2
12 2 n3 > n5
13 3 n3 > n2 > n1
14 3 n3 > n2 > n4
15 3 n3 > n5 > n6
16 2 n4 > n2
17 2 n4 > n5
18 2 n4 > n6
19 3 n4 > n2 > n1
20 3 n4 > n2 > n3
21 2 n5 > n3
22 2 n5 > n4
23 2 n5 > n6
24 3 n5 > n3 > n2
25 4 n5 > n3 > n2 > n1
26 2 n6 > n4
27 2 n6 > n5
28 3 n6 > n4 > n2
29 3 n6 > n5 > n3
30 4 n6 > n4 > n2 > n1
The whitespace was added manually to separate the paths into groups that start, in turn, from each different node to improve readability.
Graph traversal using the normalized "edges" table design
Start by populating the "edges" table with the data that defines the graph shown in the section Undirected cyclic graph (just as above) but this time using the scheme that represents each undirected edge in only one direction.
delete from edges;
alter table edges drop constraint if exists edges_chk cascade;
alter table edges add constraint edges_chk check(node_1 < node_2);
insert into edges(node_1, node_2) values
('n1', 'n2'),
('n2', 'n3'),
('n2', 'n4'),
('n3', 'n5'),
('n4', 'n5'),
('n4', 'n6'),
('n5', 'n6');
The choice of the definition of the constraint, "node_1 < node_2" is arbitrary; "node_2 < node_1" would work just as well as long as rows are populated appropriately. The inequality ensures both that the same node isn't recorded in both columns and that when a particular edge is recorded as, say, ('a', 'b'), it cannot also be recorded in the other direction as ('b', 'a').
The WHERE clause predicate in the non-recursive term that, in the SQL above, is written simply as node_1 = start_node, must now be written thus:
node_1 = start_node or node_2 = start_node
And the WHERE clause predicate in the recursive term that, in the SQL above, is written simply as e.node_1 = terminal(p.path), must now be written thus:
e.node_1 = terminal(p.path) or e.node_2 = terminal(p.path)
Further, the SELECT list item in the non-recursive term that, in the SQL above, is written simply as array[start_node, node_2], must now be written thus:
array[
start_node,
case
when start_node = node_1 then node_2
when start_node = node_2 then node_1
end case]
And the SELECT list item in the recursive term that, in the SQL above, is written simply as p.path||e.node_2, must now be written thus:
p.path
||
case
when terminal(p.path) = e.node_1 then e.node_2
when terminal(p.path) = e.node_2 then e.node_1
end case
A corresponding adjustment must be made in the predicate that prevents cycles. It would bring unacceptable clutter to write three similar CASE expressions explicitly in place and so an encapsulation function is preferred. First, do this:
cr-other-node.sql
drop function if exists other_node(text, text, text) cascade;
create function other_node(this_node in text, node_1 in text, node_2 in text)
returns text
language plpgsql
as $body$
begin
-- Will get "case not found" error if no match.
case
when this_node = node_1 then return node_2;
when this_node = node_2 then return node_1;
end case;
end;
$body$;
And now recreate the "find_paths()" procedure:
cr-find-paths-with-nocycle-check-alt.sql
drop procedure if exists find_paths(text) cascade;
create procedure find_paths(start_node in text)
language plpgsql
as $body$
begin
-- See "cr-find-paths-with-pruning.sql". This index demonstrates that
-- no more than one path has been found to any particular terminal node.
drop index if exists raw_paths_terminal_unq cascade;
commit;
delete from raw_paths;
with
recursive paths(path) as (
select array[start_node, other_node(start_node, node_1, node_2)]
from edges where node_1 = start_node or node_2 = start_node
union all
select p.path||other_node(terminal(p.path), e.node_1, e.node_2)
from edges e, paths p
where (e.node_1 = terminal(p.path) or e.node_2 = terminal(p.path))
and not other_node(terminal(p.path), e.node_1, e.node_2) = any(p.path) -- <<<<< Prevent cycles.
)
insert into raw_paths(path)
select path
from paths;
end;
$body$;
Invoke it and observe the results just as was shown above:
call find_paths(start_node => 'n1');
\t on
select t from list_paths('raw_paths');
\t off
Compare the results from the two approaches. You will see that they are identical.
Even with the "other_node()" function encapsulation of the CASE logic, the SQL for the "edges" representation that avoids denormalization is unacceptably more verbose, and correspondingly harder to understand, than is the SQL for the denormalized "edges" representation. The representation that this section uses, and the SQL that it brings, are therefore discarded.
But there is another, and more critical, reason to discard the approach that avoids denormalization in the "edges" table: the execution plan.
It's obviously quicker to identify a single row with an identity predicate on a column with an optimal index for such a predicate than it is to identify the row using the OR combination of two predicates, only one of which, of course, will identify the row. Moreover, because the primary key is defined on the column list "(node_1, node_2)" and because the SQL for the denormalized "edges" table approach restricts only on the leading column, the execution plan can use the index that enforces the primary key constraint.
Look at the output of the \d meta-command for the "edges" table:
Column | Type | Collation | Nullable | Default
--------+------+-----------+----------+---------
node_1 | text | | not null |
node_2 | text | | not null |
Indexes:
"edges_pk" PRIMARY KEY, lsm (node_1 HASH, node_2)
Check constraints:
"edges_chk" CHECK (node_1 <> node_2)
This output is for the approach that uses denormalization. The output for the table that avoids denormalization is identical except for the spelling of the constraint. It uses the < inequality operator whereas the output shown here uses the <> operator. The HASH index on the "node_1" column reflects the LSM storage method (effectively an index-organized table) down in the Spanner-inspired distributed storage layer—which is as good as it gets for the identity predicate on "node_1".
In contrast, the identity predicate on "node_2" will have no index support, Of course, you could create a secondary index on the "node_2" column. But such an index brings its own bad consequences for the performance of data-changing statements in a distributed SQL database.
How to implement early path pruning
The design concept here is to implement the pseudocode (as specified in the section that specifies the semantics of the recursive CTE) for the SQL for the approach that uses the denormalized "edges" table approach.
Then, because the intermediate data that is inaccessible to user-SQL when you use a recursive CTE is now exposed in ordinary tables, the pruning code can be added.
First re-define the "edges_chk" constraint and re-populate the "edges" table as specified in the section Graph traversal using the denormalized "edges" table design.
Next, drop and re-create the "find_paths()" procedure like this:
cr-find-paths-with-pruning.sql
drop procedure if exists find_paths(text, boolean) cascade;
create procedure find_paths(start_node in text, prune in boolean)
language plpgsql
as $body$
<<b>>declare
n int not null := 0;
begin
-- Will be created at the end when "prune" is true.
drop index if exists raw_paths_terminal_unq cascade;
commit;
-- Emulate the non-recursive term.
delete from raw_paths;
delete from previous_paths;
insert into previous_paths(path)
select array[start_node, e.node_2]
from edges e
where e.node_1 = start_node;
insert into raw_paths(path)
select r.path from previous_paths r;
-- Emulate the recursive term.
loop
delete from temp_paths;
insert into temp_paths(path)
select w.path||e.node_2
from edges e
inner join previous_paths w on e.node_1 = terminal(w.path)
where not e.node_2 = any(w.path); -- <<<<< Prevent cycles.
get diagnostics n = row_count;
exit when n < 1;
if prune then
delete from temp_paths
where
(
-- Prune all but one path to each distinct new terminal.
path not in (select min(path) from temp_paths group by terminal(path))
)
or
(
-- Prune newer (and therefore longer) paths to
-- already-found terminals.
terminal(path) in
(
select terminal(path)
from raw_paths
)
);
end if;
delete from previous_paths;
insert into previous_paths(path) select t.path from temp_paths t;
insert into raw_paths (path) select t.path from temp_paths t;
end loop;
commit;
if prune then
create unique index raw_paths_terminal_unq on raw_paths(terminal(path));
commit;
end if;
end b;
$body$;
Notice how the tables are used:
- The "raw_paths" table is used in place of the in-memory representation of the in-progress eventual final result set that the implementation of the recursive CTE uses.
- The "temp_paths" and "previous_paths" tables implement the transient in-memory representations that are shown in the pseudocode that specifies how the recursive CTE works. (See the section Semantics) subsection of the main account of the recursive CTE ).
- The "raw_paths_trg" trigger is not needed to support the implementation. Rather, its purpose is only pedagogic.
Notice that the early pruning logic is guarded by an IF test that does, or omits, the pruning according to the value supplied for a boolean input formal parameter.
- It implements a
DELETEstatement whoseFROMitem is the "temp_paths" table. This logic simply cannot be expressed using an explicit recursive CTE for the simple reason that its implementation does not expose the structure that the "temp_paths" table emulates for manipulation by user-written SQL. - The first leg of the pruning predicate eliminates all but the first path in the path sorting order to any particular node in the set that the current repetition of the recursive term has found. This restriction is expressed in terms of the content of the "temp_paths" table. Notice that the choice to retain the path that sorts first is the same choice that the "filter_paths()" algorithm uses. This ensures a deterministic comparison between the result produced by the straightforward "find_paths()" implementation that uses the recursive CTE directly, followed by "restrict_to_shortest_paths()", and the result produced by the early pruning implementation of "find_paths()".
- The second leg of the pruning predicate eliminates paths that the current repetition has found whose terminal is identical to that of any path found by any of the previous repetitions. These previously found paths are necessarily shorter than those that the present repetition finds. (See the code that inspects the "repeat_nr" column in the "raw_paths" table, and the associated explanation of its observed content, below.) This restriction is expressed in terms of the content of the under-construction ultimate result set in the "raw_paths" table—which also is not exposed by user-written SQL when the explicit recursive CTE is used.
First invoke this version of "find_paths()" without pruning:
call find_paths(start_node => 'n1', prune => false);
and confirm, using "list_paths()" that it produces the same set of paths as does the version of "find_paths()" that the section Graph traversal using the denormalized "edges" table design described.
\t on
select t from list_paths('raw_paths');
\t off
Now inspect the "repeat_nr" column, thus:
select
repeat_nr as "repeat #",
path
from raw_paths
order by repeat_nr, path[2], path[3], path[4], path[5], path[6];
This is the result:
repeat # | path
----------+---------------------
0 | {n1,n2}
1 | {n1,n2,n3}
1 | {n1,n2,n4}
2 | {n1,n2,n3,n5}
2 | {n1,n2,n4,n5}
2 | {n1,n2,n4,n6}
3 | {n1,n2,n3,n5,n4}
3 | {n1,n2,n3,n5,n6}
3 | {n1,n2,n4,n5,n3}
3 | {n1,n2,n4,n5,n6}
3 | {n1,n2,n4,n6,n5}
4 | {n1,n2,n3,n5,n4,n6}
4 | {n1,n2,n3,n5,n6,n4}
4 | {n1,n2,n4,n6,n5,n3}
The whitespace was added manually to separate the paths into groups that were produced by the same repeat of the recursive (or iterative, if you prefer) logic.
It confirms what you can, with sufficient intellectual effort, predict. But it's always sensible to confirm (or at least, fail to refute) such predictions by empirical observation.
Each successive repeat of the recursive term produces a set of paths each of which is one step longer than those produced by the previous repeat.
The design of the early pruning algorithm relies on this fact.
Next invoke it with pruning and confirm that this produces the same set of paths that were produced by "restrict_to_shortest_paths()" on the raw results produced by the version of "find_paths()" that the section Graph traversal using the denormalized "edges" table design described.
It's better to do this by executing a programmatic assertion than simply by eyeballing two nominally identical result sets.
First, recreate the basic "find_paths()" procedure by executing the code shown at cr-find-paths-with-nocycle-check.sql. (This is the version that uses the WITH clause recursive statement straightforwardly and that cannot, therefore, implement early pruning). Then invoke it.
call find_paths(start_node => 'n1');
call restrict_to_shortest_paths('raw_paths', 'shortest_paths');
Now reinstate the version that implements early pruning by executing the code shown at cr-find-paths-with-pruning.sql and invoke this.
call find_paths(start_node => 'n1', prune => true);
At this stage, the "shortest_paths" table contains the set of shortest paths from node "n1" produced by post factum filtering of the set of all paths from "n1". And the "raw_paths" table contains the set of shortest paths from node "n1" produced by early pruning. These two sets ought to be identical. Test this assertion with the procedure "assert_shortest_paths_same_as_raw_paths()":
call assert_shortest_paths_same_as_raw_paths();
The assertion holds.